Золотое сечение в дизайне

Идеальный треугольник и пентаграмма

Идеальным называют равнобедренный треугольник, основание которого относится к длине стороны как 1/3. То есть, снова-таки соблюдается золотое сечение. Начертить треугольник с идеальным соотношением сторон несложно. Удобнее циркулем, но можно обойтись и линейкой.

Золотой треугольник, правило его построения и применение в создании интерьера, например

Построение такое. На прямой от точки A трижды откладываем отрезок произвольной длины. Эту длину обозначим O. Получаем точку B. Через нее проводим прямую, перпендикулярную отрезку AB. На этой линии в обе стороны от точки B откладываем величину O. Получаем две точки d и d1. Соединяем их с точкой A. Вот и получили треугольник, стороны которого относятся как 1,62. Проверить это можно, если отложить при помощи циркуля длину основания на боковой стороне (точка C). Вторая проверка — противолежащий угол составляет 36°.

Построение пентаграммы несколько сложнее. Ее вписываем в круг, без циркуля не обойтись.

Центр окружности обозначаем O, через него проводим прямую до пересечения с окружностью. Одну из точек пересечения обозначаем A. Отрезок OA — диаметр окружности.
Находим середину отрезка OD, ставим точку E. Из центра окружности вверх до пересечения с окружностью восстанавливаем перпендикуляр. Это точка D.

Построение пентаграммы

Соединяем точки E и D. При помощи циркуля откладываем на радиусе точку C. Отрезок СD равен длине отрезка ED. Циркулем замеряем длину отрезка ED. Иглу ставим в точку E, ведем грифель до пересечения с радиусом. Вот и получили точку C.
Длинна отрезка DC — сторона пентаграммы. Замеряем ее, при помощи циркуля переносим на окружность. Для этого циркулем с отложенным расстоянием ставим еще четыре точки на окружности, поочередно соединив их, получаем пентаграмму.

Вот что интересно, если вершины полученной пентаграммы использовать для прорисовки звезды, она будет состоять из идеальных треугольников.

Фибоначчи и его задачи

После Фибоначчи осталось большое число задач, которые были очень популярны среди математиков и в последующие столетия. Мы с вами рассмотрим задачу о кроликах, в решении которой и используются числа Фибоначчи.

Кролики – не только ценный мех

Фибоначчи задал такие условия: существует пара новорожденных кроликов (самец и самка) такой интересной породы, что они регулярно (начиная со второго месяца) производят потомство – всегда одну новую пару кроликов. Тоже, как можно догадаться, самца и самку.

Эти условные кролики помещены в замкнутое пространство и с увлечением размножаются. Оговаривается также, что ни один кролик не умирает от какой-нибудь загадочной кроличьей болезни.

Надо вычислить, сколько кроликов мы получим через год.

В начале 1 месяца у нас 1 пара кроликов. В конце месяца они спариваются.
Второй месяц – у нас уже 2 пары кроликов (у пара – родители + 1 пара – их потомство).
Третий месяц: Первая пара рождает новую пару, вторая пара спаривается. Итого – 3 пары кроликов.
Четвертый месяц: Первая пара рождает новую пару, вторая пара времени не теряет и тоже рождает новую пару, третья пара пока только спаривается. Итого – 5 пар кроликов.

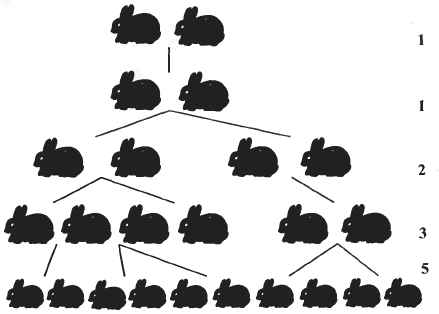
Число кроликов в n
-ый месяц = число пар кроликов из предыдущего месяца + число новорожденных пар (их столько же, сколько пар кроликов было за 2 месяца до настоящего момента). И все это описывается формулой, которую мы уже привели выше: F n = F n-1 + F n-2
.

Таким образом, получаем рекуррентную (пояснение о рекурсии
– ниже) числовую последовательность. В которой каждое следующее число равно сумме двух предыдущих:

1 + 1 = 2
2 + 1 = 3
3 + 2 = 5
5 + 3 = 8
8 + 5 = 13
13 + 8 = 21
21 + 13 = 34
34 + 21 = 55
55 + 34 = 89
89 + 55 = 144
144 + 89 = 233
233+ 144 = 377

Продолжать последовательность можно долго: 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987 . Но поскольку мы задали конкретный срок – год, нас интересует результат, полученный на 12-ом «ходу». Т.е. 13-ый член последовательности: 377.

Ответ в задаче: 377 кроликов будет получено при соблюдении всех заявленных условий.

Одно из свойств последовательности чисел Фибоначчи очень любопытно. Если взять две последовательные пары из ряда и разделить большее число на меньшее, результат будет постепенно приближаться к золотому сечению
(прочитать о нем подробнее вы сможете дальше в статье).

Говоря языком математики, «предел отношений a n+1
к a n
равен золотому сечению»
.

Еще задачи по теории чисел

Найдите число, которое можно разделить на 7. Кроме того, если разделить его на 2, 3, 4, 5, 6, в остатке получится единица.
Найдите квадратное число. О нем известно, что если прибавить к нему 5 или отнять 5, снова получится квадратное число.

Почему вы должны использовать золотое сечение в своем декоре

Asbe/Getty Images

СмитБрюинз/Twenty20

Купите эти товары сейчас: Старинный журнальный столик – стулья Accent

Все мы слышали о золотом сечении. Скорее всего, он хранится вместе со всеми остальными вашими воспоминаниями о уроках рисования в колледже или вы случайно прочитали об этом, просматривая статью в газете пару недель назад. Но знаете ли вы, что золотое сечение также играет роль в том, что мы считаем «хорошим» дизайном интерьера? Прежде чем мы начнем, немного напомним: золотое сечение — это математическая последовательность, которая повторяется снова и снова. в природе. Было обнаружено, что это соотношение — 1:1,61, если быть точным, — объясняет все, от пропорций человеческого тела до формирования музыкальных последовательностей и архитектурных формул, восходящих к древним грекам и римлянам. Несмотря на то, что оно имеет различные применения, большинство людей считают, что использование этого соотношения делает вещи более эстетичными для окружающих.

СмитБрюинз/Твенти20

Купите эти продукты сейчас: Тафтинговая скамья – стеклянный журнальный столик

Ваша мебель будет сбалансирована

Любой, кто когда-либо привозил домой новый диван, знает, насколько сложной может быть расстановка мебели. Во-первых, вы уверены, что в одном месте он будет отлично смотреться, но когда вы его поместите, что-то пойдет не так

Прежде чем вы это узнаете, вы уже несколько раз перемещали один и тот же диван по своей гостиной, только чтобы он вернулся туда, где вы начали! В следующий раз избегайте всех хлопот, заранее принимая во внимание пропорции комнаты. Хотя никогда не помешает снять мерки, если вам не хочется снимать рулетку, держите в уме пропорцию 2:3 при обустройстве пространства

Для начала визуально разделите пространство на две части. секции – более крупная, занимающая две трети пространства и вмещающая мебель, которая определяет основное назначение комнаты, и последняя треть, на которую приходится второстепенная функция, такая как отдельная зона отдыха или место для хранения.

Гетти Изображений

Купите эти продукты сейчас: Стул-стол – вытяжка

Выбор цвета станет проще простого

Если вы некоторое время читали Freshome, скорее всего, вы слышали о правиле 10-30-60 при выборе цветовой палитры. Однако вы можете не знать, что эти расчеты не являются произвольными. Они основаны на соотношении 1:1,618. Для тех, кто не в курсе, правило 10-30-60 гласит, что хорошо спроектированное пространство должно состоять из трех цветов. Во-первых, доминирующий цвет, который должен покрывать около 60% пространства и обычно используется в таких областях, как стены и пол. Далее следует вторичный цвет, который занимает 30% площади и обычно используется для мебели. Наконец, более смелый акцентный цвет должен занимать последние 10% и использоваться в небольших предметах декора. Правило 10-30-60 — это не все, что может предложить соотношение с точки зрения цвета.

Гетти Изображений

Купите эти продукты сейчас: Секционный диван — лампа

Подвесной декор не займет много времени

После того, как вы расставили мебель и выбрали цвета, пришло время перейти к тому, что кажется самым простым элементом дизайна, но часто может быть самым сложным. Правильно, куда повесить предметы декора

Прежде чем делать в стенах кучу ненужных дырок от гвоздей, примите во внимание правило третей. После того, как вы выбрали стену, на которую поместите свое произведение искусства, мысленно представьте эту стену как сетку, на которую наложены две линии, делящие ее на равные трети по горизонтали и вертикали

asbe/Getty Images

Купите эти товары прямо сейчас: Стул Accent – обои Bricks

Вы можете легко вносить коррективы

Вот холодная, суровая правда: хотя важно учитывать соотношение при декорировании, оно может не работать идеально в 100% случаев. У нас есть несколько советов, которые помогут вам справиться с такими ситуациями: Многие приведенные нами примеры работают с предположением, что комнаты были прямоугольными

Возможно, вам придется внести некоторые коррективы, чтобы соответствовать вашему пространству.

Бруклинберри/ Двадцать20

Купите эти товары прямо сейчас: Поднос для ванной — увеличительное зеркало для макияжа

Если подумать, золотое сечение действительно удивительно.

Золотой прямоугольник и спираль Фибоначчи

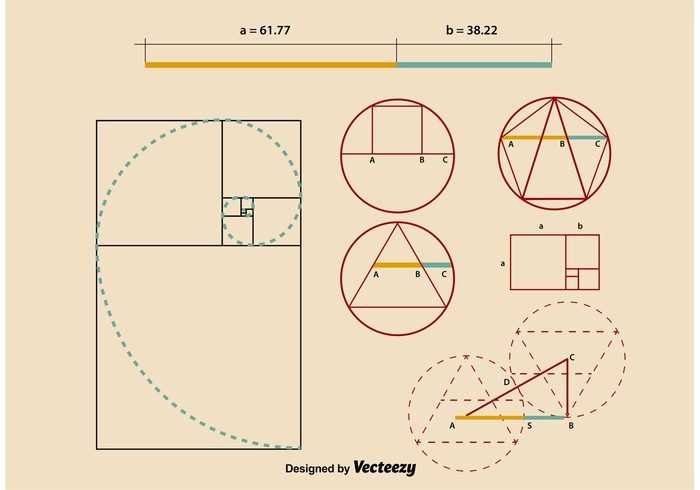
Еще одну любопытную параллель между числами Фибоначчи и золотым сечением позволяет провести так называемый «золотой прямоугольник»: его стороны соотносятся в пропорции 1,618 к 1. А ведь мы уже знаем, что за число 1,618, верно?

Например, возьмем два последовательных члена ряда Фибоначчи – 8 и 13 – и построим прямоугольник со следующими параметрами: ширина = 8, длина = 13.

А затем разобьем большой прямоугольник на меньшие. Обязательное условие: длины сторон прямоугольников должны соответствовать числам Фибоначчи. Т.е. длина стороны большего прямоугольника должна быть равной сумме сторон двух меньших прямоугольников.

Так, как это выполнено на этом рисунке (для удобства фигуры подписаны латинскими буквами).

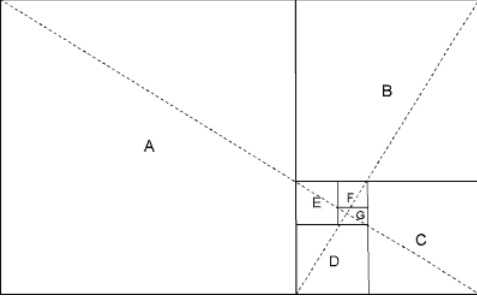
Кстати, строить прямоугольники можно и в обратном порядке. Т.е. начать построение с квадратов со стороной 1. К которым, руководствуясь озвученным выше принципом, достраиваются фигуры со сторонами, равными числам Фибоначчи. Теоретически продолжать так можно бесконечно долго – ведь и ряд Фибоначчи формально бесконечен.

Если соединить плавной линией углы полученных на рисунке прямоугольников, получим логарифмическую спираль. Вернее, ее частный случай – спираль Фибоначчи. Она характеризуется, в частности, тем, что не имеет границ и не изменяет формы.

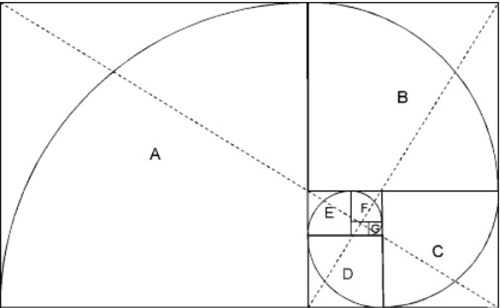
Подобная спираль часто встречается в природе. Раковины моллюсков – один из самых ярких примеров. Более того, спиральную форму имеют некоторые галактики, которые можно разглядеть с Земли

Если вы обращаете внимание на прогнозы погоды по телевизору, то могли заметить, что подобную спиральную форму имеют циклоны при съемке их со спутников

Любопытно, что и спираль ДНК подчиняется правилу золотого сечения – соответствующую закономерность можно усмотреть в интервалах ее изгибов.

Такие удивительные «совпадения» не могут не будоражить умы и не порождать разговоры о неком едином алгоритме, которому подчиняются все явления в жизни Вселенной. Теперь вы понимаете, почему эта статья называется именно так? И двери в какие удивительные миры способна открыть для вас математика?

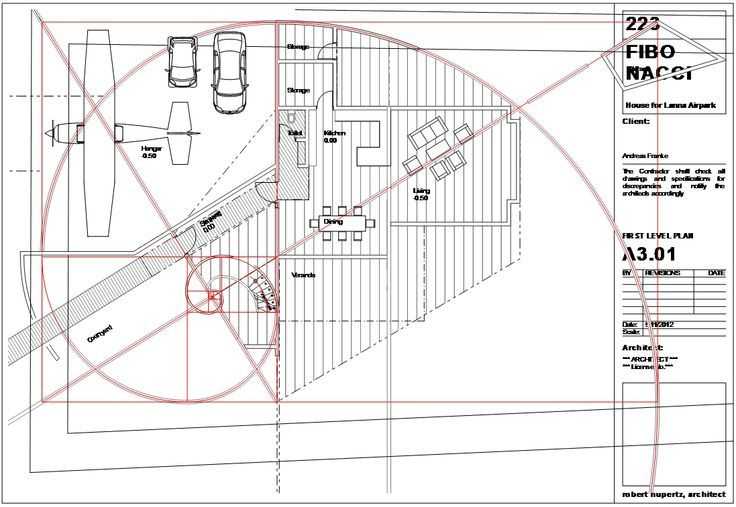
Золотое сечение в мировой архитектуре

Убедиться в существовании идеальной пропорции можно на примерах различных архитектурных объектов, в том числе — возведенных во времена античности и средневековья. Королевские резиденции и усыпальницы, храмы и церкви, построенные с учетом универсального стандарта, встречаются в разных странах по всему миру.

Древнеегипетские прототипы

Одним из главных сооружений Древнего Египта является пирамида Хеопса, проектировщики которой, вероятно, имели четкое представление об особенностях рассматриваемого принципа. С геометрической точки зрения единственное из сохранившихся чудес Света, расположенное в Гизе, представляет собой треугольник с золотым сечением — можно представить строительство объекта в виде соотношения строго вертикальной центральной оси и половины длины основания, где сопоставление гипотенузы и меньшей стороны даст уже знакомое значение 1,62. Стоит отметить, что комплексу приписывают различные мистические свойства — начиная с улучшения вкуса питьевой воды и заканчивая ускорением темпов роста растений, оказавшихся внутри. Однако подобные утверждения не имеют под собой научного обоснования или рационального объяснения.

Архитектура Древней Греции

Одним из самых известных памятников древнегреческой культуры является Парфенон — храм, построенный в пятом веке до нашей эры. Здесь для получения искомого коэффициента достаточно соотнести высоту и ширину объекта. Ученые отмечают, что для достижения абсолютного значения и устранения погрешностей нужно вычесть из вертикали 14 см, добавив их к горизонтальной длине

Принимая во внимание архитектурные особенности, можно сделать вывод о том, что подобные расчеты были осознанно выполнены его проектировщиками — Калликратом и Иктином, которые решили слегка сузить верхнюю часть фасада. Тем не менее общие пропорции здания остаются соблюденными и в полной мере отвечают концепции золотого сечения.

Российская архитектура

Используя числовую последовательность Фибоначчи в качестве матрицы для анализа различных сооружений, можно также выделить явные примеры соблюдения подобной последовательности в наиболее известных и узнаваемых зданиях России.

Золотое сечение в архитектурных решениях Москвы

Одним из знаковых представителей можно считать корпус МГУ на Воробьевых горах, возведенный уже после окончания войны. На момент строительства это был самый высокий из реализованных проектов, предусматривающий наличие пяти композиционных групп, увенчанных центральной башней. В конфигурации четко прослеживается присутствие прямоугольного треугольника с гипотенузой, проходящей через пристройки и угол основания, что в совокупности дает нужное соотношение. Аналогичные пропорции прослеживаются и в проектах за авторством Матвея Казакова, будь то Кремлевское здание сената, Дом союзов, Пречистенский дворец или Голицынская больница. Также универсальной формулой пользовался архитектор Василий Баженов, одним из примеров работ которого является дом Пашкова (XVIII в.)

Золотое сечение в архитектуре Санкт-Петербурга

Еще один образец, демонстрирующий преимущества универсальной формулы — Исаакиевский собор, основная часть которого вписана в прямоугольник со сторонами 400 и 248. Гармоничный визуальный образ памятника также дополняет купол, выполненный с соблюдением идеальных пропорций. Среди других выдающихся зданий северной столицы можно отметить такие объекты, как:

Кунсткамера. Возведенная в 1718 г. под руководством немецкого архитектора Георга Маттарнови, она предусматривает наличие двух трехэтажных корпусов, с возведенной между ними многоярусной башенной конструкцией куполообразной формы. По всей высоте башни прослеживается четкий равнобедренный треугольник, а соотношения длин корпусных зданий и различных уровневых высот также дают результат, равный коэффициенту золотого сечения.
ТД Эсдерс и Схейфальс. Еще одна знаменитая постройка, законченная в 1907 году, отличается гармоничной визуализацией благодаря наличию шпиля, венчающего один из углов, и строгому следованию высотным величинам.
Дом Советов. Созданный на основе проекта Л. Троцкого в 1941-м, объект характеризуется наличием двух корпусов по пять этажей каждый, а также центрального 14-колонного портика, дополненного оригинальным скульптурным ансамблем. Длина здания — 1472 ед., что при делении на универсальный коэффициент дает четкий размерный ряд, которому соответствуют различные декоративные и функциональные элементы. Треугольник, вписанный в центр, идеально совпадает с вершиной, тогда как гипотенузы упираются в крайние точки крыльев, расположенных по бокам.

Регулирующие линии

Очень важное правило для любого стиля сада — будь то итальянский, французский или супер современный сад с техническими новинками. Линии помогают увидеть композицию по частям и целом, скорректировать

Они соединяют дом и сад, переходят с дома в сад и наоборот

Они соединяют дом и сад, переходят с дома в сад и наоборот.

Линии создаются деревьями, растениями, архитектурными формами, водоемами, ограждениями и домом. Они бывают простыми и сложными, прямыми, горизонтальными, вертикальными, диагональными. С помощью растений жесткие прямые линии дома в стиле модерн можно смягчить растениями, характерными для японского сада — сакурой, кленами, хризантемами.

При высаживании молодых растений важно помнить о том, как они будут изменятся во времени. Ведь вся композиция создана для Вас и должна во всех своих ипостасях доставлять радость созерцания именно Вам

Числа Фибоначчи в визуальном искусстве и дизайне

Золотая спираль, основанная на последовательности чисел Фибоначчи, является одним из универсальных принципов построения пропорций. Лежащее в ее основе золотое сечение было известно еще в государствах Древнего Востока, но особую популярность оно приобрело в эпоху Возрождения. Великие скульпторы и живописцы того времени начали применять золотую спираль для построения художественной композиции, пропорций различных объектов, в том числе человеческого тела. Золотое сечение сегодня используется как одна из моделей для гармоничного распределения объектов в кадре (в фото- и киноискусстве), элементов плакатов и т.д.

В компьютерную эру золотое сечение (золотая спираль) и числа Фибоначчи также нашли свое применение в визуальном искусстве, в частности, 2D/3D-моделировании и веб-дизайне:

Решетка Фибоначчи применяется для эффективного наложения точек на двухмерные и трехмерные объекты, например сферу или многогранники. Таким способом можно выполнить высокоточную огранку ювелирных камней или построить визуальную модель молекулярных решеток некоторых веществ.

Решетка Фибоначчи на трехмерной фигуре (сфере)

На основе числовой последовательности Фибоначчи строится один из вариантов фракталов — самоподобных фигур. Эту математическую модель можно использовать в компьютерной графике для построения ветвящихся объектов (ветвей, корней деревьев, русел рек, кристаллов и т. д.).
Золотое сечение применяется в веб-дизайне для разметки страниц некоторых сайтов или веб-приложений. Элементы интерфейса, организованные таким способом, образуют визуально привлекательную и удобную рабочую область.
Фрактальная геометрия, основанная в том числе на закономерности Фибоначчи, является самостоятельным направлением визуального искусства. Она применяется в аудиовизуальных инсталляциях, мэппингах и т.д.

Использование Золотого сечения

Считается, что Золотое сечение использовалось как минимум 4000 лет в изобразительном искусстве и дизайне. В более современные времена Золотое сечение можно наблюдать в музыке, искусстве и дизайне. Применяя аналогичную рабочую методологию, вы можете привнести те же ощущения дизайна в вашу собственную работу.

Давайте посмотрим на пару примеров.

Древнегреческая архитектура использует Золотое сечение для определения нужных размеров

Древнегреческая архитектура использовала Золотое сечение, чтобы определить идеальные размерные соотношения между шириной здания и его высотой, размером портика и даже положением колонн, поддерживающих конструкцию.

Конечный результат – здание, которое ощущается полностью пропорционально. Неоклассическое архитектурное движение также повторно использовало эти принципы.

Леонардо да Винчи широко использовал Золотое сечение

Леонардо да Винчи, как и многие другие художники на протяжении веков, широко использовал Золотое сечение для создания идеальных композиций. В «Тайной вечере» фигуры располагаются в нижних двух третях (большей из двух частей Золотого сечения), и положение Иисуса идеально строится путем расположения золотых прямоугольников по всему холсту.

Есть также многочисленные примеры Золотого сечения в природе – вы можете наблюдать это вокруг себя. Цветы, морские раковины, ананасы и даже соты.

Создание золотого сечения

Создание золотого прямоугольника довольно просто, и начинается с базового квадрата. Выполните следующие действия, чтобы создать свое собственное Золотое сечение:

01. Нарисуйте квадрат

Начните с рисования квадрата любого размера. Сторона этого квадрата будет формировать длину “короткой стороны” прямоугольника.

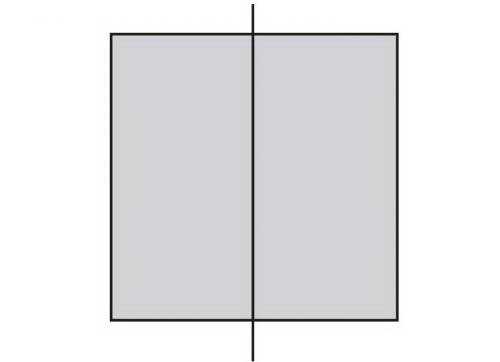
Разделите ваш квадрат пополам вертикальной линией по центру. В результате получится два прямоугольника.

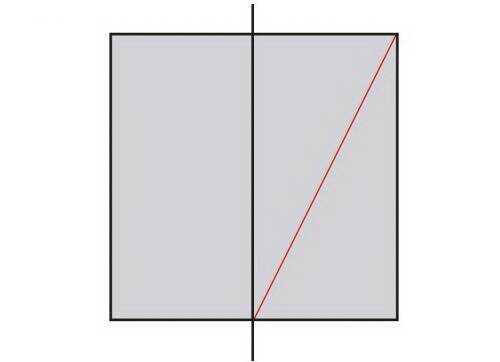
В одном из этих прямоугольников нарисуйте прямую линию от одного угла до противоположного угла.

04. Поверните линию

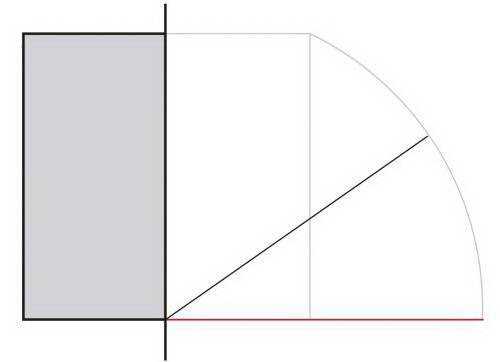
Поверните эту линию, поворачивая от нижней (или верхней) точки, пока она не совпадет с нижней частью первого прямоугольника.

05. Создайте новый прямоугольник

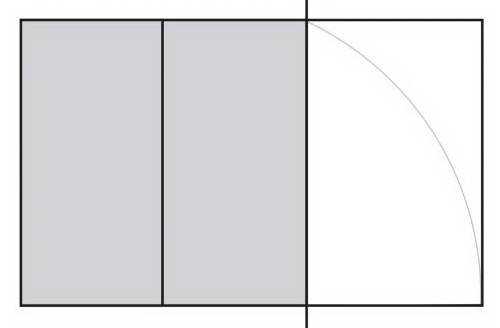
Создайте прямоугольник, используя новую горизонтальную линию и исходный прямоугольник в качестве направляющих. Это будет ваш золотой прямоугольник.

Использование Золотого сечения проще, чем вы думаете. Есть несколько быстрых трюков, которые вы можете использовать, чтобы представить идею в своих макетах.

Быстрый способ

Если вы когда-либо сталкивались с «Правилом третей», вы будете знакомы с идеей, что, разделив область на равные трети как по вертикали, так и по горизонтали, пересечение линий обеспечит естественный фокус для фигуры.

Фотографов учат размещать ключевой объект на одной из этих пересекающихся линий, чтобы получить идеальную композицию, и тот же принцип можно использовать в макетах страниц, макетах веб-сайтов и в постерах.

Правило третей может быть применено к любой фигуре, если вы примените его к прямоугольнику с пропорциями приблизительно 1: 1,6, вы получите золотой прямоугольник, что делает композицию еще более приятной для глаз.

Полная реализация Золотого сечения

Если вы хотите полностью внедрить Золотое сечение в свой дизайн, вы можете сделать это, обеспечив соотношение между областью содержимого и боковой панелью (например, в дизайне веб-сайта) в соотношении 1: 1,61.

Можно округлить это число вверх или вниз на одну или две точки, чтобы получить числа с пикселями или точками. Поэтому, если у вас есть область содержимого 640 пикселей, боковая панель 400 пикселей будет достаточно хорошо соответствовать золотому сечению.

Использование Золотого сечения в макете веб-страницы обеспечивает естественный, приятный результат.

Конечно, вы также можете разделить области контента и боковой панели вверх, используя одинаковое соотношение, и связь между верхним колонтитулом, областью контента, нижним колонтитулом и навигацией также может быть разработана с использованием того же базового золотого коэффициента.

Вместо заключения

Когда мы готовили этот материал, наш редактор вспомнил диалог из старой детской книжки «В лабиринте чисел» — кажется, он идеально подходит для финала статьи о числах Фибоначчи.

Приводим его полностью:

Чит недоумённо пожал плечами. Ряд как ряд! Что в нём интересного?

— Не скажи, — живо возразила Ари. — У чисел Фибоначчи куча удивительных свойств. Взять, например, дерево — из тех, что ветвятся ежегодно. Если на втором году жизни у него два ответвления, то на третьем их уже будет три, на четвёртом — пять, на пятом — восемь, на шестом — тринадцать и так далее. А ведь всё это числа Фибоначчи! С тем же рядом связано и расположение листьев на ветке, и количество завитков, образованных семечками подсолнуха, чешуйками сосновой шишки или ананаса… Как видишь, природа широко пользуется числами Фибоначчи.

— A люди? — неожиданно выпалил Чит. — Они-то ими пользуются?

— Где людям угнаться за природой! Долгое время о числах Фибоначчи просто не знали. Но и потом они оставались безработными много столетий. И только в нынешнем, двадцатом веке им нашлось наконец дело. Во-первых, подобно булевой алгебре и теории множеств, числа Фибоначчи используются в вычислительных и думающих машинах. Во-вторых, с их помощью были решены некоторые математические задачи. Ну да о них ты узнаешь в своё время. Как ещё сработает этот удивительный числовой ряд, сказать трудно. Ясно одно: бесполезных открытий не бывает.

Правило золотого сечения в фотографии. Золотое сечение — что это?

Одним из самых мощных композиционных правил в фотографии является правило золотого сечения, которое еще называют “божественной пропорцией”. Согласно ему, кадр необходимо разделить на девять частей — двумя линиями по горизонтали и двумя по вертикали. На пересечении линий образовываются четыре точки, называемые узлами внимания — это самые активные области на фотографии, на которые приходится больше всего внимания. Именно там и на самих линиях необходимо размещать главные объекты и расставлять акценты.

Композиция должна состоять из нескольких частей — таких, чтобы вся горизонталь отрезка имела в соотношении большую и меньшую части, одинаково пропорциональные к основной длине. Параметры золотого сечения составляют 1:0.618:1.

История возникновения правила

Свои истоки правило берет с древнейших времен: первые упоминания о нем найдены в трудах Евклида “Начала”, которые были написаны около 300 лет до н. э. Там он применял принцип деления отрезка в крайнем и среднем отношении для построения правильного пятиугольника, который тоже называют золотым.

По другой версии, за закон золотого сечения человечество должно быть благодарно Пифагору, который сам сделал это открытие и поведал о нем остальным. Но Пифагор был не только известным математиком, но и мистиком, поэтому открытие данного правило обросло мистическими значениями и потусторонними смыслами

Последователи великого мыслителя не брали во внимание такие домыслы, а лишь руководствовались этим правилом для создания прекрасных скульптур, сооружений и барельефов

Интересный факт: эти золотые пропорции использовались в жизни древних людей, а точнее — египтян. По правилам золотого сечения сконструированы пирамида Хеопса, египетский храм Парфенон, барельефы и даже украшения, которые найдены в гробнице Тутанхамона.

Поучаствовал в поиске идеальных пропорций и итальянский математик Леонардо Фибоначчи, которому удалось выявить удивительную закономерность. Случилось это примерно в 1200 году. Ученый тогда заметил, что в природе и окружающей нас действительности есть определенная схема, которой все подчиняется и которая очень приятна человеческому глазу. Он поставил в ряд определенные числа и заметил, что каждая часть последовательности является результатом сложения двух предыдущих. Благодаря этой последовательности мир увидел знаменитые спираль и сетку Фибоначчи, которые используют в построении грамотной композиции до сих пор.

Пропорции и «золотое сечение»

Даже в случае использования вышеперечисленных принципов оформления для каждого растения, чем-то выделяющегося, и для каждого декоративного элемента в саду необходимо найти свое место, а также определить его оптимальные размеры. Садовые пространства, отдельные растения, живые изгороди, насаждения и конструктивные многолетние садовые элементы должны оптимально сочетаться по своим размерам друг с другом и с садом в целом. Для этого необходимо соблюдать определенные пропорции.

При соблюдении этого правила сад будет радовать глаз гармонией или приятным сочетанием контрастов. В то же время симметрия — неизменный спутник гармонии, тогда как другие пропорции необходимы для создания контрастов. Применение принципа «золотого сечения» позволяет добиться гармоничного сочетания пропорций. Указанные пропорции использовались уже в античной архитектуре. Что касается сада, то это понятие может относиться к пропорциям высот, размерам поперечного сечения деревьев или элементов здания, а также расстояниям между отдельными точками.

«Золотое сечение» — это вполне определенное гармоническое соотношение длин отрезков, которые образуются в результате деления прямой, лежащей в ее точке. Это соотношение составляет примерно 5/8 длины линии. Применительно к территории сада это означает, что в саду обязательно должна быть точка, которая бросается в глаза. Может служить отдельным большим деревом, отличным по всем параметрам от остальных деревьев. Теперь пришло время применить размеры этого дерева к эскизу или плану сада.

Затем из этой точки отсчета проводят две линии под прямым углом друг к другу. Длины этих линий определяют «золотое сечение». Для простоты можно сделать одну из них длиной 8 см, а другую 5 см. Естественно, первая линия может быть любой другой длины, а длина второй в этом случае должна рассчитываться с использованием указанной пропорции. В нашем примере от точки отсчета была проведена линия длиной 15 см, поэтому второй отрезок получился равным 9 см. Если теперь соединить концы этих линий вместе, получится прямоугольный треугольник.

Один из его углов в нашем примере представляет собой эффектное дерево, а два других угла должны быть отмечены строительными, декоративными или растительными элементами

С помощью «золотого сечения» в саду определяются оптимальные места для расположения привлекающих внимание объектов, будь то растения, скульптуры или строительные элементы

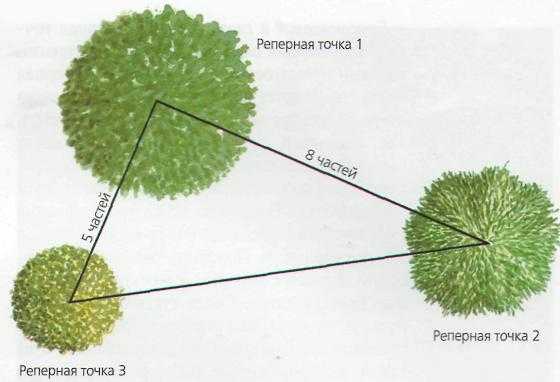
Если вы хотите правильно расположить отдельные элементы сада, следует придерживаться принципа «золотого сечения»

На основе использования принципа «золотого сечения» возможно также гармоничное сочетание строительных элементов с садовыми насаждениями

Привлекательное дерево (опорная точка 1) в сочетании с двумя другими опорными точками играет особую роль. Первая опорная точка доминирует над второй, а вторая, в свою очередь, над третьей (см рисунок). Так, например, опорными точками 2 и 3 могут быть деревья одного вида, но разного размера, посаженные в местах, соответствующих этим точкам. Также возможно использование двух или даже трех разных видов деревьев или кустарников. Подробнее размещение оценочное хорошо смотреться на открытых газовых простахах. Среди густых насаждений ориентиры должны быть отмечены одинаковыми растениями (например, выделяющимися кустами). В любом случае выбор реперных точек должен производиться очень тщательно и с учетом их соответствия друг другу.